Big O Notation

The speed and memory usage of an algorithm aren’t necessarily fixed; they might change depending on the input. So how do we express the performance of an algorithm then?

Enter Big O Notation, a powerful tool that allows us to generalize the space-time complexity of an algorithm as a function of its input size.

Let’s say we have an array of n length

$$ a = […] $$

And the following functions

$$ f_1(a) = 1 + a[0] $$

Simply returns the first element of array plus one

$$ f_2(a) = sum(a) $$

Return the sum of all elements in array

$$ f_3(a) = pair(a) $$

Each possible pair combination

All of those algorithms take an array.

const sum = arr => arr.reduce((acc, el) => acc + el, 0)
const pair = arr => 
  arr.map(mainEl => arr.map(secondEl => [mainEl, secondEl]))

const arrayWithLengh = length => Array.from({length}, (v, k) => k+1)


const a = arrayWithLengh(10)
const a100Elements =  arrayWithLengh(100)
const a1000Elements = arrayWithLengh(1000)

const f1 = (x) => 1 + x[0]
const f2 = (x) => sum(x) 
const f3 = (x) => pair(x)

// Computed time For 1 Element
f1(a) // ~0.021ms (for 1 element)
f2(a) // ~0.046ms (for 1 element)
f3(a) // ~0.065ms (for 1 element)

// Computed time For 10 Elements
f1(a) // ~0.027ms (for 10 elements)
f2(a) // ~0.059ms (for 10 elements)
f3(a) // ~0.116ms (for 10 elements)

// Computed time For 100 Elements
f1(a100Elements) // ~0.021ms (for 100 elements)
f2(a100Elements) // ~0.071ms (for 100 elements)
f3(a100Elements) // ~3.644ms (for 100 elements)

// Computed time For 1000 Elements
f1(a1000Elements) // ~0.020ms (for 1000 elements)
f2(a1000Elements) // ~0.263ms (for 1000 elements)
f3(a1000Elements) // ~96.810ms (for 1000 elements)

You can see that the speed of each algorithm is directly related to the length of the array. Big O notation help us understand and compare the complexity of each algorithm.

$$ f_1(a) = 1 + a[0] $$

Time Complexity: **O(1)**


          **Constant**

$$ f_2(a) = sum(a) $$

Time Complexity: **O(N)**


              **Linear**

$$ f_3(a) = pair(a) $$

Time Complexity: O(N²)

          **Quadratic**

Asymptotic Analyses

An example of What is Asymptotic Analyses? is a function f4 that contains all other functions

$$ f_4(a)= f_1(a) + f_2(a) + f_3(a) $$

This means that f4 have the complexity of

$$ O(1) + O(n) + O(n^2) ∴ O(n^2 + n + 1) $$

But notice how n and 1 is irrelevant when compared with n², so in this case we just say O(n²)

Most Used Notations

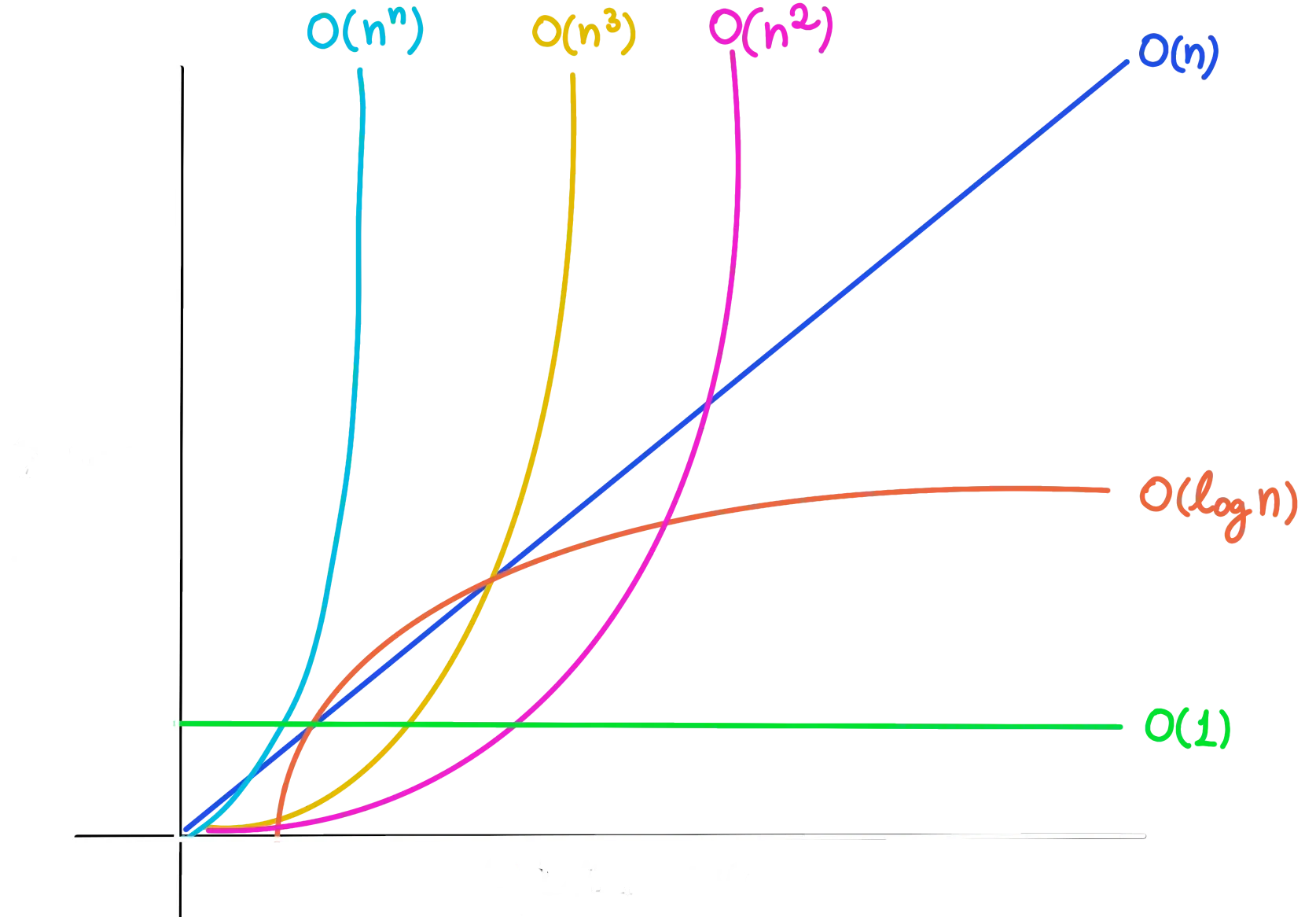
$$ O(1) \ \scriptsize \color{gray}Constant $$

$$ O(log\space n) \ \scriptsize \color{gray} Logaritimic $$

$$ O(n) \ \scriptsize \color{gray} Linear $$

$$ O(n * log\space n) \ \scriptsize \color{gray} Linearithimic $$

$$ O(n^2), O(n^3), O(n^4) \ \scriptsize \color{gray} Quadratic, Cubic, Polynomial $$

$$ O(2^n) \ \scriptsize \color{gray} Exponential $$

$$ O(n!) \ \scriptsize \color{gray} Factorial $$

🔥 Big O Notation always refer to the worst case scenario

Few Examples

O(25) → O(1)

O(2n) → O(n)

O(n² + 2n) → O(n²)

O(n³ + log(n) + 3) → O(n³)

O(n + m) → O(n + m)

O(2n + m) → O(n + m)

The most common Big O Notations are:

O(1) → Constant | Accessing a memory address

O(log n) → Logarithmic | Binary Search

O(n) → Linear | Iterating an Array

O(n log n) → Linearithimic | Iterating an Array

O(n²) → Quadratic | Nested Iterations

O(2^n) → Exponential | Nested Iterations

O(n!) → Factorial | Generate all permutations of a list

Time Complexity

A measure of how fast an algorithm runs, time complexity is a central concept in the field of algorithms. It’s expressed by using Big O notation.

Space Complexity

A measure of how much auxiliary memory an algorithm takes up, space complexity is a central concept in the field of algorithms and it’s also expressed using Big O notation

Flash Cards